Hermitian inner product

Une multitude de produits de qualité pour des projets réussis ! Faites le meilleur choix ! Hermitian Inner Product. That is, it satisfies the following properties, where denotes the complex conjugate of.

This means, by de nition, that (;) : V V ! So, an inner product is a sesquilinear form. The takeaway is that the first argument is conjugate not the second.

Wave motion can be used to analyze plane structures with small defects such as cracks and obtain. There are hermitian inner product -related words in total, with the top most semantically related being hilbert space, dot product, scalar, dimension and norm.

You can get the definition(s) of a word in the list below by tapping the question-mark icon next to it. The words at the top of the list are the ones most associated with hermitian inner product, and as you go down the relatedness becomes more slight. VII, the physical Hilbert space, which is required for the physical interpretation of the model, is introduce by defining a new inner product, called the physical inner product, in a certain subspace of H. Offre spéciale - comprimés gratuits!

An inner product on a vector space V over a field K (which must be either the field ℝ of real numbers or the field ℂ of complex numbers) is a function (,): V × V K such that, for all kk ∈ K and ������, �� ∈ V, the following properties hold: 1. The concepts of orthogonality, orthogonal family of vec-tors, orthonormal family of vectors, and orthogonal com-plement of a set of vectors, are unchanged from the Eu- clidean case (Definition ). Linear: For all u,v,w V and any real scalar 2. Conjugate Symmetric: For all u,v V 3. Stack Exchange network consists of 1QA communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers. Euclidean n-space, and the dot product is called the standard inner product on Rn.

Complex Inner Product Spaces The Euclidean inner product is the most commonly used inner product in. However, on occasion it is useful to consider other inner products. H is of type SymTridiagonal.

It is a linear operator on a vector space V that is equipped with positive definite inner product. In physics an inner product is usually notated as a bra and ket, following Dirac. Let Bbe a non-unital algebra. Band unique numbers λ. First of all, the eigenvalues must be real!

In the light of certain preliminary studies, these two families seem to have an empty overlap. In this paper, we will show that whenever the interaction potentials are chosen to be. The dot product of two vectors is the sum of their components multiplied one by one and added (possibly with complex conjugation if they are complex).

Physical transformations as unitary operators In quantum mechanics, physical transformations such as rotations, translations, and time evolution correspond to maps that take states to other states. These maps should be linear and preserve the inner product, that is they should act as unitary operators. By the property of inner product space, we must have Tw( ) =for all wV∈ hence T = 0. Let T be linear transformation sending (ab,) into (−ba,).

This follows using property (2) above of the inner product. The inner product "ab" of a vector can be multiplied only if "a vector" and "b vector" have the same dimension. The outer product "a × b" of a vector can be multiplied only when "a vector" and "b vector" have three dimensions. For any change of basis matrix P, the Gram ma-trix of h,i with respect to the new basis is P⇤GP.

We write the complex inner product = vHu. A matrix Ais hermitian if AT = A. For example any symmetric matrix of real entries is also hermitian. Then there is a unitary. Theorem Let Abe a hermitian matrix.

If A is equal to its adjoint under the unitary inner product, then A is hermitian : A = At (11) I t is also convenient to give a name to the opposite situation: Definition. It is not hard to verify that the indicated limit exists (for Cauchy sequences fx mg;fy ng), and gives a hermitian inner product on the completion.

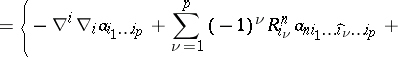
The completion process does nothing to a space which is already complete.