Hermitian scalar

Inner product spaces may be defined over any fiel having "inner products" that are linear in the first argument, conjugate-symmetrical, and positive-definite. I know that positive definite symmetric matrices (in euclidean vector spaces) are always invertible.

Soit E un espace vectoriel complexe. For a quantum field theory the introduction into. That depends on what field the scalar comes from. Full-text: Open access.

Operators and their properties 2. A physical state is represented mathematically by a ve. Hermitian ) inner product, on Cn. A scalar λ and a nonzero vector v are referred to, respectively, as an eigenvalue and corresponding eigenvector for L if and only if L(v) = λv.

University Math Help. Advanced Algebra O. First of all, the eigenvalues must be real!

The physical subspaces are bounded by zero eigenvalues, exceptional points or for theories with more than complex scalar fields also by singularities. For n =U = u (a scalar ) with λ = u. For a Kähler metric, the Riemannian scalar curvature is equal to twice the Chern scalar curvature. For such metrics, if they exist, the Chern scalar curvature would have the same geometric meaning as the Riemannian scalar curvature. Recently, Liu–Yang showed that if this equivalence of.

That is, it satisfies the following properties, where z^_ denotes the complex conjugate of z. This paper generalizes a rigidity result of complex hyperbolic spaces by M. A comparative analysis of a model of complex scalar field φ and real scalar field χ with interaction for the real and purely imaginary values of coupling g in perturbative and non-perturbative regions is provided. Leading dimension of dA.

B: COMPLEX array on GPU device. The scalar product is defined as above. The properties of the scalar product are easy to derive from the integral. It equals zero iff.

We may also derive the Schwartz inequality. Linear operators take vectors in the space int.

This page aims to provide an overview and some details on how to perform arithmetic between matrices, vectors and scalars with Eigen. Divides the hermitian matrix through a scalar.

Swaps the contents of the hermitian matrices. Inserts the value t at the j-th element of the i-th row.

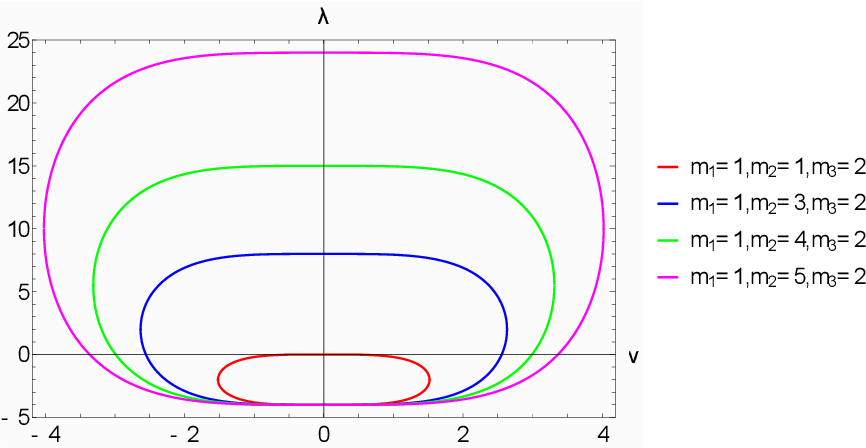
The limiting ruled surfaces, together with the corresponding spin structures, are described in Theorem 3. Then H (M, C7(K)) =i =2. By arguments similar to those in Proposition 1. I suggest you develop a strong grounding in complex numbers and linear algebra to understand hermitian matrices and there applications. Here’s a list of all the ideas necessary to understand vector spaces, basis and hermitian matrices Vector Space.

Recall that the scalar λ is an eigenvalue of the (square) matrix A if and only if there is a column vector X such that. Each of these matrices has some special properties, which we will study. If either operand is a scalar, each entry in the other matrix is multiplied by that scalar.

Matrix Power ^ At least one operand must be a scalar, and any matrix must be square. I have not yet found a use for raising a scalar to a matrix. Only scalar physical quantities correspond to basic observables ( hermitian square matrices) within the relevant Hilbert space L. Physical vectors may also be considere which correspond to operators mapping a ket into a vector of kets (i.e., an element of some Cartesian power of L ).